Mis notas y resumen (Jesús Díaz)
La geometría analítica a finales del XVI, a manos de Descartes y Desargues tendió puentes con el álgebra y permitió una clasificación sistemática de las curvas.
1. Algunos preliminares geométricos
Un ángulo está inscrito en una circunferencia si el vértice está sobre ella y los lados la cortan, abarcando entre ellos un cierto arco. La medida de este arco es siempre la mitad de la del ángulo. Para demostrar esto, supongamos en primer lugar que uno de los lados pasa por el centro de la circunferencia. Resulta que si ningún lado del ángulo inscrito pasa por el centro, o bien el centro es interior al ángulo o bien es exterior. Potencia de un punto respecto de una circunferencia (Ver Teorema de Meneleao, de Ceva)
2. Los orígenes de la geometría proyectiva
Nuestro protagonista en este origen, conocido como el teórico en la materia, Leon Battista Alberti (1404-1472), quien explicó el principio que sería la base del sistema matemático de perspectiva. El hecho, la idea, es que la sección sobre del lienzo de un cuadro, no puede ser calcada directamente, y para dibujarla hacen falta unas ciertas reglas geométricas. Formuló un problema importante: ¿cuál es la relación entre dos secciones de un mismo objeto tomadas desde diferentes puntos de vista?
Sobre lo que es una propiedad proyectiva
La idea es que la propiedad de ser un círculo o un cuadrado no se mantiene a través de proyecciones ni secciones (porque dos secciones no son siempre paralelas), lo que quiere decir que no lo es lo que en adelante llamaremos una propiedad proyectiva. Tampoco se conservan las distancias, ángulos, paralelismo. La única propiedad proyectiva que de momento tenemos es la de ser una línea recta: tres puntos alineados siempre se convierten en tres puntos alineados. El estudio de las propiedades proyectivas de las figuras se llama geometría proyectiva.
Las conicas y la geometría proyectiva
Se denomina sección cónica (o simplemente cónica) a todas las curvas resultantes de las diferentes intersecciones entre un cono y un plano; si dicho plano no pasa por el vértice. Las cónicas de Apolonio es una obra compuesta por ocho libros, el octavo libro se ha perdido.
Las distintas posiciones del plano en relación con el eje del cono dan lugar a las distintas clases de cónicas. Si el plano corta a todas las generatrices, la cónica es una elipse. En cambio, si es paralelo a una de ellas, resulta ser una parábola y en todos los demás casos se obtiene una hipérbola.
Se puede encontrar, para cada género de cónica, una propiedad compartida por todos sus puntos. Con ella, la curva puede ser estudiada por sí misma, prescindiendo de las superficies que la generan. Dejamos como ejercicio buscar esta propiedad para la elipse, la hipérbola y la parábola.
Los puntos de la elipse son aquellos cuya suma de distancias a otros dos F y F* (llamados focos) es constante.
La hipérbola está formada por los puntos cuya diferencia de distancias a los focos es constante.
La parábola es el conjunto de puntos del plano que equidistan de un punto llamado foco y de una recta llamada directriz.
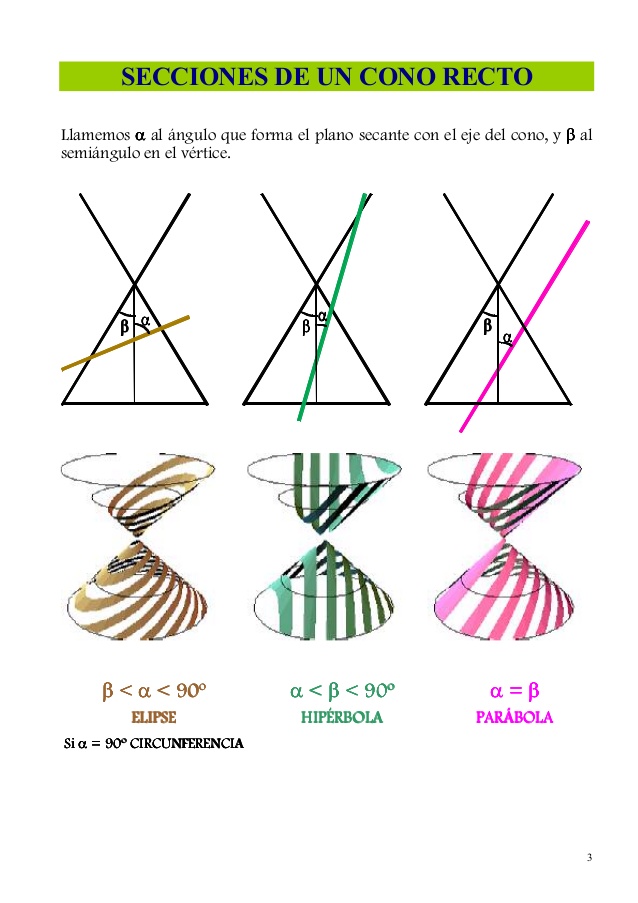
Vemos que con proyecciones cualquier cónica se puede convertir en cualquier otra proyectándola desde un punto exterior a su plano y cortando el haz de rectas así obtenido con otro plano. (A excepción de la cónica degenerada, si el plano pasa por el vértice del cono, se obtiene un par de rectas)
