Fundamentos de Lógica Pura
Camino a una renovación de la Lógica Pura
Jesús Díaz, 22 Enero 2021
Observación: Ya en los textos de Euclides, Arquímedes y Apolonio la noción de demostración no es nada diferente a la de nuestros días.
Ir a Fundamentos de Lógica Pura (parte II)
Introducción
Ideas:
- El problema de La Naturaleza de los números naturales y la fundamentación de la aritmética.
- Reducir la aritmética y el análisis a la lógica, definiendo las nociones aritméticas a partir de nociones puramente lógicas y deduciendo los axiomas aritméticos a partir de principios lógicos.
De nociones puramente lógicas a nociones aritméticas.
De principios lógicos a axiomas aritméticos.
Ideografía: cada símbolo tiene un significado único.
ideograma: Signo gráfico que representa un concepto o idea de forma sintética y no por análisis de sonidos o formas.
Fases:
- Desarrollo de la lógica sobre la base de un formalismo o ideografía. Cuantificadores y variables ligadas (análisis, conceptos y métodos en la lógica actual)
- Los fundamentos de la aritmética. Los números se dicen de los conceptos. Para cada concepto P definir el concepto de segundo orden «equivalente a P». En general, x pertenece a los números naturales si y solo sí hay algún concepto P tal que x es el número P.
- Semántica. Deducir con una ideografía las leyes fundamentales de la aritmética a partir de los principios lógicos.
- Fundamentación de la geometría. Teoría semántica.
Función y concepto
El sentido y la referencia de las expresiones nominales (nombres) y su extensión a todo tipo de expresiones lingüísticas.
Un enunciado (o sentencia) tiene como referencia su valor booleano y como sentido el pensamiento objetivo.
Enunciado, referencia (Valor veritativo(booleano) o propiedad o característica del objeto)
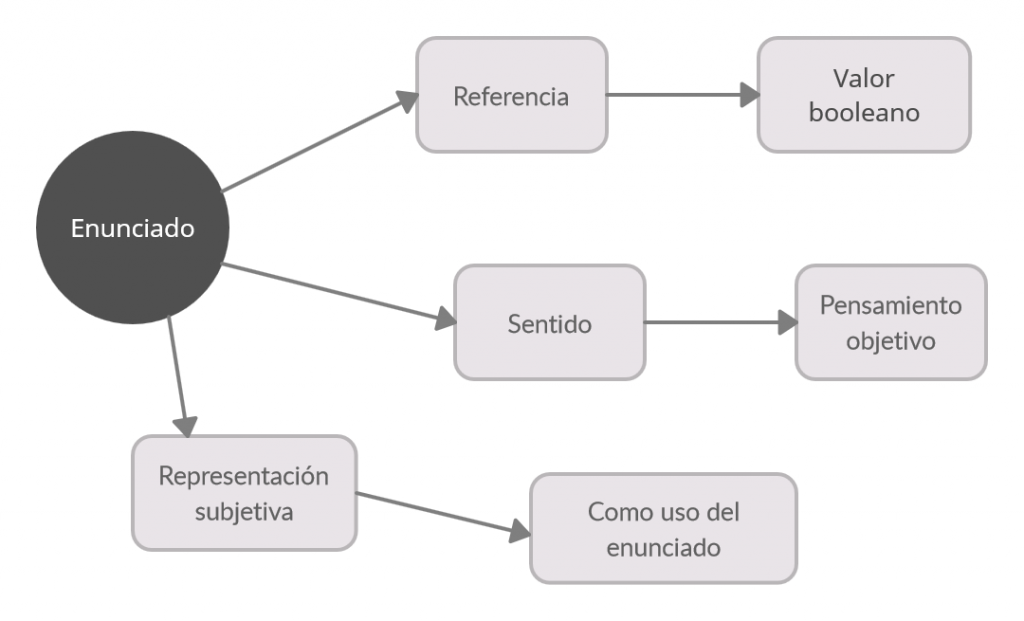
Enunciado, sentido, pensamiento objetivo. ¿Qué es pensamiento objetivo?
OBJETO Y FUNCIÓN
Objetos –> Cosas: Plantas, animales, números naturales, etc.
Functor –> designa una función.
Funciones:
- Relaciones
- Operaciones de N
- Conceptos
- Nombre.
- Enunciado.
- Referencia.
- Sentido (del signo o expresión).
El objeto al que una expresión se refiere o designa es su referencia.
Limite(1+1/n)^n y Sum(1/n!) estas expresiones tienen la misma referencia, el número real e, pero tienen distinto sentido.
Expresión y objeto o referencia al objeto. (referirse al objeto por una propiedad suya)
Los valores veritativo son Objetos. Los enunciados son Nombres de los objetos.
El sentido de los enunciados y de los objetos.
Sentido y referencia a las expresiones functoriales, a las expresiones de conceptos.
La referencia de una expresión conceptual no es la extensión del concepto sino el concepto mismo.
Concepto, propiedad, característica
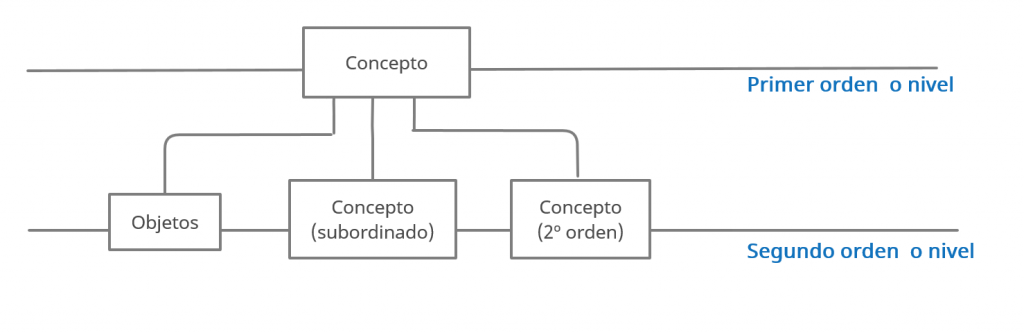
Un concepto está subordinado a otro concepto si todos los objetos que caen bajo el primer concepto caen también bajo el segundo.
Caer bajo un concepto (ser elemento de una clase). Estar subordinado a otro concepto (estar incluido en otra clase).
Distinción entre propiedad y característica. Propiedad, característica, concepto y definición.
¿Qué es un concepto?, ¿Qué es una definición?, ¿Qué es un principio (postulado)?, ¿Qué es un axioma?
Propiedad y característica.
Un objeto tiene una propiedad si cae bajo el correspondiente concepto. Pero un concepto es una característica de otro concepto si entra en su definición y, por tanto, el primer concepto es una propiedad de todos los objetos que caen bajo el segundo.
Ordenes o niveles y conceptos.
 Noción de recorrido de una función. ¿Extensión de un concepto?
Noción de recorrido de una función. ¿Extensión de un concepto?
- Dominio, contradominio.
- Clase de díadas.
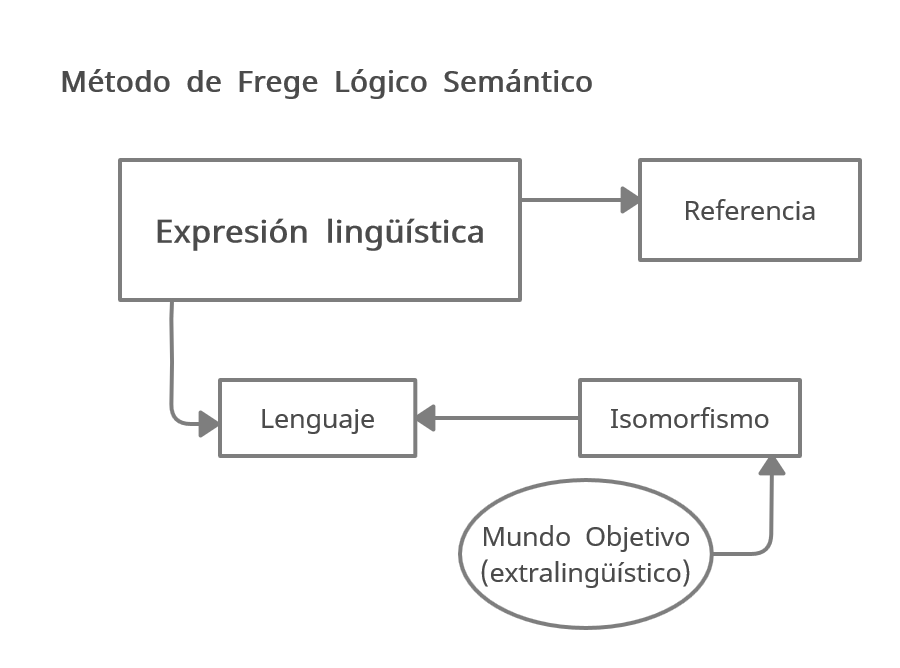
- signos sin contenido. Propiedades a un sólo contenido del signo.
- cosa esencial: El mismo contenido y no su forma.
- Una realidad. Un hecho. Reflejo de vida propia, conciencia.
- Un número.
- Un signo numérico.
- Una referencia a un signo numérico.
La función y el número, naturaleza de la función
- Coincidencia completa
- Concordancia parcial
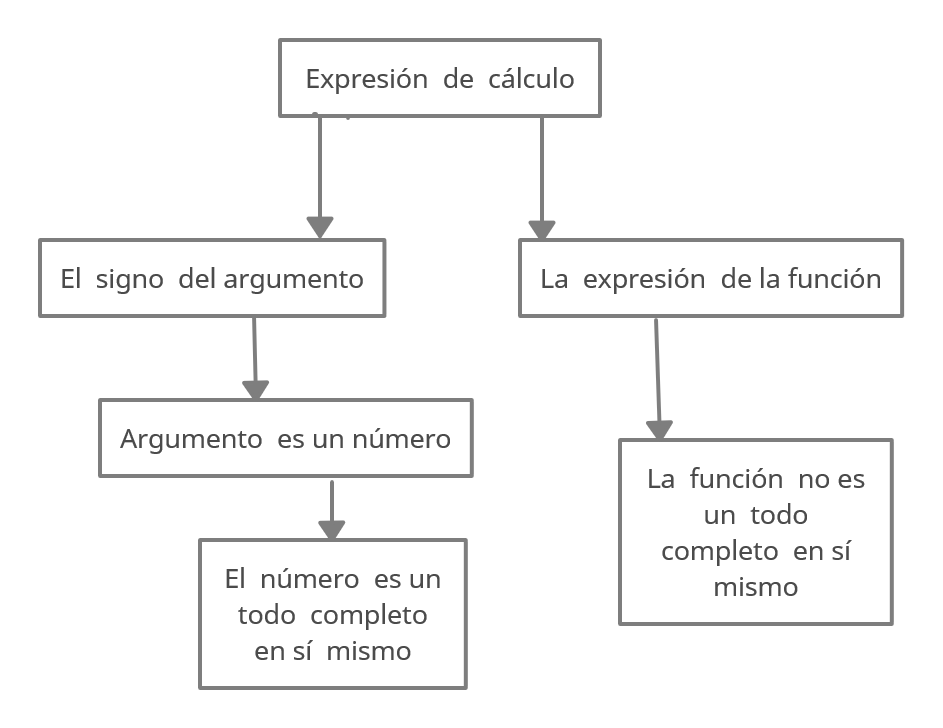
- Se amplió el círculo de las operaciones de cálculo.
- Se amplió el círculo, argumento y valor de la función al ser admitidos los números complejos.
El número -1 tiene la propiedad de que su cuadrado es 1.
El número -1 es una raíz cuadrada de 1.
El número -1 cae bajo el concepto de la raíz cuadrada de 1.
- La parte completa en sí misma.
- La parte complemento (es no-saturada).
| SÍMBOLO | DESIGNACIÓN |
| VER | VER = VERDADERO EXIGE, IMPONE que su valor sea siempre verdadero |
| AFI | AFI = AFIRMACIÓN afirmamos una expresión o parte |
| AFIVER | AFIVER = AFIRMAMOS que ese valor es verdadero |
| NEG | NEG = NEGACIÓN |
Ejemplo: «AFIVER 2 + 3 = 5» No solo atribuimos un valor veritativo verdadero sino que también lo afirmamos.
«VERNEG 2^2 = 5» se referirá a lo verdadero
y con AFIVERNEG 2^2 = 5 afirmamos que 2^2 = 5 no es lo verdadero o que 2^2 no es 5.
Como 2^2 no es 5, VERNEG 2 es lo verdadero, porque VER 2 es lo falso. Aquí 2 no es lo verdadero.
Enunciados: «2^2 = 5 no es lo verdadero», «2 es lo falso», «2 no es lo verdadero»
Representar la generalización
Objeto. Función. Argumento. Letra. Valor de la función.
Función generalizada si valor es verdadero toma valor verdadero en otros casos toma el valor falso.
No todo objeto es raíz cuadrada de 1.
Hay objetos que no son raíz cuadrada de 1.
No para cada argumento es el valor de la función lo verdadero.
No para cada argumento es el valor de la función x^2 = 1 lo falso.
Hay por lo menos una raíz cuadrada de 1.
Funciones de 1er orden, son funciones cuyo argumentos son objetos.
Funciones de 2do orden, son funciones cuyos argumentos son y deben ser funciones.
Expresión. Función. Desmembrar el signo compuesto de un objeto en una parte saturada y otra no-saturada.
Ejemplo: descomponer el signo «3 > 2» de lo verdadero en «3» y «x > 2»
Podemos seguir descomponiendo la parte no saturada «x > 2» del mismo modo en «2» y «x > y», donde ahora «y» indica el lugar vacío, que antes había sido llenado por «2».
Con x > y tenemos una función con dos argumentos y con 3 > 2 tenemos el valor de esa función para los argumentos 3 y 2.
Funciones con un argumento las hemos llamado conceptos. Funciones con dos argumentos las llamamos relaciones.
Distinguimos entre las funciones de un argumento las de primero y de segundo grado.
Una función con dos argumentos puede ser de grado igual o de grado desigual. Una función de grado desigual es, por ejemplo, el cociente diferencial.
1. Función de grado desigual.
2. Funciones de grado igual:
- Funciones de 1er grado
- Funciones de 2do grado. ( f(g[1]), f y g indican los argumentos)
Leyes generales para las funciones. Expresión artificial «función». Funciones singulares de segundo grado.
Sentido y referencia.
¿Es la igualdad una relación?, ¿es una relación entre objetos?, ¿o bien entre nombres o signos de objetos? Esto último es lo que supuse en mi ideografía.
Relación entre objetos. Relación entre nombres o signos de objetos.
Enunciados:
a = a y a = b , diferente valor cognoscitivo
a = a vale a priori (según Kant), puede denominarse analítico.
Ahora la forma a = b no siempre puede justificarse a priori.
Igualdad. Relación. Nombres. Referencias. Criterio veritativo.
a = b los signos o nombres “a” y “b” se refieren a lo mismo. Por lo tanto en la igualdad se afirmaría una relación entre ellos. La relación existiría entre los nombres o signos si estos designan algo.
Relación inducida por la conexión. Dos signos. Cosa designada. Conexión arbitraria. Suceso u objeto como signo.
El enunciado a = b puede referir al modo de designación.
Diferencia entre signos:
- Como objeto, su forma.
- No como signo
- Modo de designación
Diferencia entre objetos:
Valor cognoscitivo.
Diferencia de signos. Diferencia en el modo de darse
Diferencia de signos. Diferencia en el modo de darse lo designado.
Designaciones distintas. Esos nombres indican al mismo tiempo el modo.
Un signo: un nombre, unión de palabras, signo escrito
Lo designado o la referencia del signo.
Lo designado va unido al sentido del signo en el cual se halla contenido el modo de darse.
La REFERENCIA de las expresiones serían ciertamente la misma, pero no sería el mismo su SENTIDO.
Signo. Nombre. Nombre propio. Con referencia un objeto determinado.
Designar un único objeto. Designación compuesta de varias palabras u otro tipo de signos.
El sentido de un nombre propio. La referencia, queda sólo parcialmente iluminada.
Un conocimiento completo de la referencia implicaría que de cada sentido dado, pudiéramos indicar inmediatamente si le pertenece o no.
Representar:
- Conexión regular
- Signo
- Sentido
- Referencia (objeto)
Mientras la referencia siga siendo la misma, pueden tolerarse estas oscilaciones del sentido:
“Aristóteles era originario de Estagira”
Y otro sentido distinto:
“El maestro de Alejandro Magno originario de Estagira”
Así pues, por el hecho de que se conciba un sentido, no se tiene con seguridad una referencia.
Uso de las palabras
Se puede querer hablar solo de su referencia. Se puede querer hablar de las palabras mismas. Se puede querer hablar solo de su sentido.
Palabras de otro en estilo directo.
Representar: palabras propias, palabras del otro, referencia corriente
Las comillas
Un carácter que se halla entre comillas no debe ser tomado en su referencia usual.
Representar: palabra, referencia (habitual), referencia (indirecta), sentido (habitual), sentido (indirecto).
Modo de conexión de signo, sentido y referencia.
Representar: referencia y sentido, signo, representación, perceptible, persona, [imagen, interna, externa], recuerdos, sentimientos, a quién pertenece, en qué momento, palabra, sentido, [asociar, modo].
Nombre propio. Referencia, objeto mismo.
Tres niveles: palabras, expresiones o frases enteras.
Representaciones. Sentido. Referencia.
Pensamiento (como contenido objetivo).
Un enunciado contiene un pensamiento. Sentido y la referencia de un enunciado asertivo completo.
El pensamiento no puede ser la referencia del enunciado, por el contrario, deberemos concebirlo con su sentido.
Quien no admita una referencia no podrá afirmar ni negar de ella un predicado.
Enunciado: sentido, referencia, valor veritativo.
Nombre propio: sentido, referencia, valor veritativo.
Por valor veritativo de un enunciado entiendo la circunstancia.
Concepto. Relación. Objeto.
Un juicio de un pensamiento es el reconocimiento de su verdad.
La forma del enunciado asertivo. Fuerza.
La relación del pensamiento con lo verdadero. Sentido -valor veritativo-modo propio-descomposición.
La relación del todo a la parte en el enunciado con su referencia. (esa relación es transferida a su referencia)
La referencia de una palabra, parte de la referencia del enunciado, y la misma palabra es parte de este enunciado.
Un enunciado se refiere en el estilo directo a otro enunciado, y en el indirecto, a un pensamiento.
Enunciados subordinados. Partes de una estructura enunciativa (es asimismo un enunciado, a saber, el enunciado principal).
Del estilo indirecto, ocurre lo contrario, los enunciados subordinados como representantes de partes del enunciado general, y, según eso, las denominan enunciados nominales, calificativos, adverbiales.
Distinguir entre enunciados que podrían ser sustituidos por un nombre, por un adjetivo calificativo o locuciones adverbiales.
Enunciados nominales abstractos “que” pertenece también el estilo indirecto, las palabras tienen una referencia indirecta.
En este caso: el enunciado subordinado tiene por referencia un pensamiento, no un valor veritativo. Por sentido, no un pensamiento, sino el sentido de las palabras “el pensamiento de que…”, el cual es sólo parte del pensamiento de toda la estructura enunciativa.
Enunciados subordinados
La referencia de un enunciado no siempre es su valor veritativo. Como excepción hay enunciados subordinados cuya referencia es un pensamiento.
Un convencimiento o una creencia es razón de un sentimiento o también puede ser razón de otro convencimiento, como ocurre en la inferencia.
Referencias indirectas y directas. Estilo indirecto y directo. Las formas subjuntivo e imperativo.
Enunciados que no tienen referencia, sino sólo un sentido.
En las subordinadas que dependen de “mandar”, “pedir”, las palabras tienen su referencia indirecta.
La referencia de uno de estos enunciados no es, pues, un valor veritativo, sino una orden, un ruego, etc.
Las palabras en su referencia indirecta.
Las interrogativas indirectas con “quién”, ”qué”, “dónde”, “cuándo”, “cómo”, “por medio de qué”, a veces se asemejan mucho a enunciados adverbiales en los que las palabras tienen su referencia usual. (se diferencia por el modo del verbo)
Caso del subjuntivo
Tenemos preguntas indirectas y referencia indirecta de las palabras, de modo que un nombre propio no puede ser sustituido en general por otro del mismo objeto.
La referencia indirecta no es un valor veritativo, sino un pensamiento (una orden, un ruego, una pregunta).
El enunciado subordinado como nombre: contexto de la estructura enunciativa.
Otros enunciados subordinados donde las palabras si tienen su referencia usual, pero sin un pensamiento como sentido, ni un valor veritativo como referencia.
Representar: enunciado subordinado, por sentido (pensamiento), referencia, enunciado principal, sujeto gramatical (sin sentido independiente), relaciones (2º miembro del enunciado).
Analizar esta estructura lingüística (lingüística pura).
El todo y la parte de un enunciado dado.
Las lenguas y su defecto al designar un objeto (pues depende de la verdad de un enunciado).
Designar realmente un objeto. Sólo designar en apariencia (sin “referencia” incluso).
Producir la ilusión de que se refieren a algo.
La subordinada. Parte de su sentido: el pensamiento.
Lenguaje lógicamente perfecto (ideografía)
Hay que exigir que cada expresión que se haya formado como nombre propio a partir de signos correctos, designe realmente, también un objeto, y que no se introduzca ningún signo como nombre propio sin que antes no se le haya asegurado una referencia.
La multivocidad (varias significaciones) de las expresiones como fuente de errores lógicos.
También la prevención frente a los nombres propios aparentes que no tienen ninguna referencia.
Nunca podrá depender de la verdad de un pensamiento el que un nombre propio tenga una referencia.
Algunos enunciados calificativos pueden servir para formar nombres propios compuestos.
Estos enunciados calificativos deben ser tomados igual que términos calificativos.
En vez de “la raíz cuadrada de 4 que es menor que 0”, puede decirse también “la raíz cuadrada negativa de 4”.
El caso en que, a partir de una expresión conceptual, se forma un nombre propio compuesto con la ayuda del artículo determinado en singular y sólo está permitido cuando cae bajo el concepto un objeto y sólo uno.
Asegurar siempre una referencia por “medio de la definición” de que su referencia será el número 0 siempre que bajo el concepto no caiga ningún objeto o más de uno.
Expresiones conceptuales. Formación. Características. Enunciados calificativos.
Expresiones conceptuales calificativas
El enunciado calificativo tienen por sentido solamente una parte de un pensamiento que, en algunos casos, puede expresarse también con un único calificativo.
Expresiones conceptuales adverbiales
Enunciados adverbiales de lugar y de tiempo pueden entonces ser utilizados para la formación de un nombre propio semejante.
| Lugares | Instantes | Intervalo temporal | ||
| Lógica | son objetos | |||
| Lingüística | nombre propio | |||
Enunciado (casos)
Considerar la parte de un sentido. El pensamiento. Condición necesaria. Referencia. La subordinada.
Antecedente junto con el consecuente exprese, uno y un solo pensamiento cuyas partes ya no son pensamientos.
Alusión lingüística explícita. Deducir del contexto.
La palabra “juicio” se usa en el mismo sentido que yo he asociado a la palabra “pensamiento”. La generalidad y sus componentes.
Condicional o antecedente y el consecuente. Alusión. Tiempo presente del verbo.
El componente que alude indeterminadamente en el enunciado principal y en el subordinado.
Expresar el sentido del subordinado en uno principal. Sentido que sea un pensamiento completo.
El sentido de la principal
El todo consistente en la principal y la subordinada es lo que contiene un pensamiento.
Los componentes comunes en el antecedente y el consecuente.
Enunciados nominales: “quien”, “lo que”.
Enunciados adverbiales: “donde”, “cuando”, “dondequiera que”, “siempre que”
Enunciados condicionales: “Quien coge barro, se ensucia”
Cuando el componente común del principal y del subordinado es designado por un nombre propio.
El subordinado, sentido y pensamiento.
La referencia de la subordinada. La referencia y el valor veritativo.
Formas y tipo de conexión de enunciados
Formas de poner un enunciado en la forma de un enunciado calificativo. El conector “y”.
- Formas lingüísticas de interpretar los enunciados (Fijarse sólo en sus valores veritativos)
- Para hacer sustituciones: en enunciados parciales
- Teniendo en cuenta el valor veritativo del todo.
Resumen
El enunciado subordinado, por lo general, no tiene por sentido ningún pensamiento, sino únicamente una parte de alguno y, en consecuencia, no tiene por referencia ningún valor veritativo.
La razón consiste: O bien en la subordinada, las palabras tienen su referencia indirecta, de modo que la referencia, y no el sentido de la subordinada, es un pensamiento. O bien en que la subordinada es incompleta pues tiene un componente que sólo alude indeterminadamente, de modo que únicamente junto con la principal puede expresar un pensamiento y entonces puede ser sustituida por otro enunciado del mismo valor veritativo.
Pensamiento principal. Pensamiento secundario. Leyes psicológicas y la unión de palabras. Pensamientos asociados a palabras.
Puede ocurrir que tengamos más pensamientos simples que enunciados.
Ver si pertenece o no el pensamiento secundario al sentido del enunciado, o bien sólo lo acompaña. (puede ser importante para saber si: una afirmación puede ser una mentira, o un juramento, un perjurio)
Tipos de pensamiento
Pensamiento ligeramente sugerido.
Pensamiento realmente expresado.
Pensamiento secundario, parte del sentido, enunciado.
Más pensamientos simples que enunciados.
Alteración del pensamiento, modificación del valor veritativo.
No siempre pueden reemplazarse enunciados del mismo valor veritativo.
El enunciado gracias a su conexión con otro, expresa más de lo que expresa por sí solo.
Expresión y número de pensamientos. Pertenencia al enunciado principal y/o al enunciado subordinado.
Expresión del pensamiento
Las palabras de la subordinada y su tipo de referencia (directa, indirecta, usual, ?)
Palabras conectadas en varios pensamientos.
Estructura enunciativa. Subordinada tomada como doble con distintas referencias, referencia que es un pensamiento, referencia que es un valor veritativo, etc.
Si el valor veritativo es toda la referencia del enunciado subordinado lo podemos sustituir por otro del mismo valor veritativo.
Expresión y correspondencia de enunciado subordinado, enunciado principal entre los enunciados aislados.
Si en una subordinada se expresa un primer pensamiento como una parte del segundo entonces podemos sustituir la subordinada por otro enunciado del mismo valor veritativo. Modificación de un segundo pensamiento, también puede afectar su valor veritativo.
Como en muchos casos expresa la subordinada no solo un pensamiento sino también una parte de otro.
En general no se puede sustituir por otro enunciado del mismo valor veritativo.
La verdad de la estructura enunciativa entera
Razones por las que no siempre se puede sustituir una subordinada por otra del mismo valor veritativo.
Razones:
- Que la subordinada no se refiere a ningún valor veritativo, al expresar sólo una parte de un pensamiento.
- Que la subordinada se refiere ciertamente a un valor veritativo, pero no se limita a esto, al comprender su sentido, además de un pensamiento, una parte de otro pensamiento.
El valor veritativo es la referencia del enunciado, el sentido del cual es un pensamiento.
Hay casos en que una subordinada no es sustituible por otra del mismo valor veritativo.
El valor cognoscitivo de “a = a” y “a = b”
Para el valor cognoscitivo, el sentido del enunciado, o sea el pensamiento expresado en él.
Considerar pensamiento expresado del valor cognoscitivo y considerar su referencia, es decir, su valor veritativo.
Si a = b, la referencia de “b” es la misma que la de “a”, y por tanto, también el valor veritativo de “a = b” es el mismo que el de “a = a”.
El sentido de “b” puede ser distinto del sentido de “a”, y con ello también será el pensamiento expresado en “a = b” distinto del expresado en “a = a”
Resumen: valor cognoscitivo de “a = a” y “a = b”
Valor cognoscitivo. Sentido. Enunciado. Pensamiento. Referencia. Valor veritativo. Juicio.
- El valor cognoscitivo de “a = a” y “a = b” es distinto.
- Importa tanto el pensamiento como su referencia, su valor veritativo.
- Si a = b, referencia de “b” = referencia de “a” y valor veritativo “a = b” = valor veritativo “a = a”
- Si sentido de “b” ≠ sentido de “a” entonces (pensamiento expresado en “a = b”) ≠ (pensamiento expresado en “a = a”). En este caso los dos enunciados tampoco tienen el mismo valor cognoscitivo.
- Si por “juicio” entendemos el paso del pensamiento a su valor veritativo, también diremos entonces que los juicios son distintos.
Diferencia entre sentido y referencia de nombres propios
Misma diferencia puede establecerse para términos conceptuales.
No confundir la división en: conceptos y objetos con la distinción entre sentido y referencia.
¡No confundir!, haciendo coincidir sentido y concepto por un lado, y referencia y objeto por otro.
En general, a cada término conceptual o nombre propio le corresponde un sentido y una referencia.
Las palabras. Sentido. Asociar una referencia a los nombres propios y términos conceptuales.
La referencia de un nombre propio es el objeto que éste designa o denomina.
Un término conceptual se refiere a un concepto si el término se emplea (tal como es conveniente) en lógica.
Los lógicos extensionales. Los lógicos intensionales.
En todo enunciado, un término conceptual puede reemplazar a otro, si ambos corresponde la misma extensión conceptual.
La inferencia y las leyes lógicas
Cómo funcionan los conceptos y sus extensiones.
La relación lógica fundamental es la de caer un objeto bajo un concepto: a ella pueden reducirse todas las relaciones entre conceptos.
Si un objeto cae bajo un concepto dado, cae bajo todos los conceptos de la misma extensión.
Las extensiones de concepto son objetos y no conceptos.
Núcleo de verdad. Función y concepto
El concepto es una función de un argumento, cuyo valor es siempre un valor veritativo.
Caer un objeto bajo un concepto. Nos interesa ver ecuaciones donde la variable represente un concepto.
La palabra “función”. Lo esencial de su significado. Referencia algo más amplia.
Un nombre de función contiene siempre lugares vacíos, por lo menos uno, para el argumento, se indica por medio de la letra “x”, que llena esos lugares vacíos.
El argumento no forma parte de la función. Tampoco la letra “x” forma parte del nombre de la función.
Lo que los llena a los nombres de función no les pertenece propiamente.
En consecuencia, la función misma la llama Frege no-saturada o necesitada de complemento. Porque para obtener una referencia completa, su nombre debe ser completado por el signo de un argumento.
Tal referencia completa la denomino objeto, y en este caso es el valor de la función para el argumento que efectúa la complementación o saturación.
Casos simples: argumento también es un objeto.
Concepto de sujeto
Naturaleza del concepto. Cuidado al hablar de concepto, pues el lenguaje oscurece el pensamiento.
Palabras como “el concepto”: tener siempre presente su inadecuación.
Objetos y conceptos son radicalmente distintos.
Los nombres propios no pueden ser utilizados como predicados.
Los conceptos no pueden estar en las mismas relaciones que los objetos.
Las palabras “sujeto” y “predicado” inducen al error de confundir las dos relaciones radicalmente distintas de caer bajo un objeto bajo un concepto y [de la] subordinación de un concepto bajo otro concepto.
Las palabras “todos” y “algunos”
Casos donde el predicado es distinto de lo que afirmamos de un objeto.
La relación de igualdad, por la que entiendo coincidencia total, identidad, sólo es concebible entre objetos, no entre conceptos.
Relación de igualdad: coincidencia total o identidad
Pues para que la referencia de un término conceptual coincida con otra referencia de un término también conceptual sea el nombre, o sea, esta referencia designe un nombre de un concepto necesita la naturaleza predicativa, la no-saturación, la posibilidad de utilizar el artículo indeterminado.
A la igualdad la llamo relación de primer orden, y sólo es concebible entre objetos.
A la relación semejante, a la que llamo de segundo orden por ser una relación entre conceptos.
Decimos que un objeto a es igual a un objeto b (en el sentido de la coincidencia completa), si a cae bajo cada uno de los conceptos bajo los que cae b, y recíprocamente.
Algo semejante para los conceptos.
Hacer que concepto y objeto intercambien sus papeles.
Si: concepto Φ y el concepto X, si cada objeto que cae bajo Φ cae también bajo X, y recíprocamente.
Añadimos lo siguiente:
La ideografía: la no-saturación del concepto (de primer orden) se representa en la ideografía de tal modo que su designación contiene por lo menos un lugar₁ vacío destinado a recibir el nombre de un objeto que ha de caer bajo el concepto.
lugar₁, debe este lugar llenarse siempre, mediante un nombre propio o un signo que sólo aluda a un objeto.
A un lado de un signo de igualdad, o de un [signo] análogo, no puede estar nunca la designación de un concepto, sino que, además del concepto, siempre habrá que designar o aludir a un objeto.
Detalles en la relación de conceptos:
- Aludir a los conceptos mediante una letra funcional. (representando la no-saturación)
- Utilizar las letras (Φ, X), que designan o aluden a conceptos, siempre sólo como letras funcionales.
Por lo tanto no se pueden igualar rigurosamente las funciones (conceptos), pues a ambos lados del signo de igualdad hay, además de las letras funcionales, algo más, que no pertenece a la función.
Designar la relación entre objetos. Estos objetos tienen por nombre “el concepto de Φ” y “el concepto de X”.
“Aquello a lo que se refieren dos términos conceptuales es lo mismo si y sólo si las extensiones de concepto correspondientes coinciden”.
Los lógicos extensionales
Consideran que lo esencial para la lógica es la referencia de las palabras, no el sentido.
Los lógicos intensionales
Tienden a fijarse mucho en el sentido. De alguna forma llaman intensión a sentido.
No tienen en cuenta que en lógica no interesa cómo se producen unos pensamientos a partir de otros sin considerar su valor veritativo.
Que hay que dar el paso del pensamiento al valor veritativo; que, más generalmente, hay que dar el paso del sentido a la referencia.
Que las leyes lógicas son ante todo leyes en el dominio de las referencias y que solo indirectamente se relacionan con el sentido.
Si nos interesa la verdad -y la verdad es el objetivo de la lógica-, debemos preguntarnos por las referencias, debemos desechar nombres propios que no designen o nombren ningún objeto, por mucho que tengan un sentido; hay que desechar términos conceptuales que no tengan referencia.
Para cada objeto debe poderse determinar si cae bajo un concepto o no.
Frege: Mis fundamentos y en la conferencia sobre teorías formalistas de la aritmética.
La referencia demuestra ser en todas partes lo esencial para la ciencia.
Los lógicos intensionales
El concepto mismo es más primario que su extensión. Pero que el concepto no debe ser concebido en tal caso como sentido del término conceptual, sino como referencia.
Los lógicos extensionales
Se aproximan más a la verdad, al poner como lo esencial de la extensión una referencia, que ciertamente no es el concepto mismo, pero que está muy estrechamente ligada a él.
Con relación a una conferencia sobre el álgebra de la lógica (lógica exacta) I, el señor Husserl le censura a Schröder su falta de claridad, al discutir las palabras sin sentido, con un sentido, con varios sentidos, sin referencia, unívoco, multívoco.
Sí hay falta de claridad pero Husserl tampoco aporta claridad. Schröder usa los componentes “sentido” y “referencia” de forma distinta al señor Frege.
El señor Frege prefiere decir “término conceptual” en vez de “nombre común”.
El nombre propio debe tener una referencia que designe o nombre un objeto.
De este modo el nombre propio se relaciona a través del sentido, y sólo de este, con el objeto.
El término conceptual debe tener un sentido y (para uso científico) una referencia. Esta referencia es un concepto.
Un término conceptual lógicamente inobjetable sin un objeto con el que se relacione es, el concepto mismo.
La lógica debe exigir tanto del nombre propio como del término conceptual que el paso de la palabra al sentido y del sentido a la referencia esté determinado sin lugar a dudas.
Sobre concepto y objeto
La palabra “concepto” se utiliza de maneras distintas, en parte en un sentido psicológico, y en parte en un sentido lógico, y en parte, quizás, en una mezcla confusa de ambos.
El uso puramente lógico de la palabra “concepto”.
Lo que es lógicamente simple no puede ser propiamente definido.
Lo lógicamente simple no está dado de antemano.
Si se descubre algo que es simple habrá que acuñar para ello una denominación, un nombre provisional por no encontrarse su nombre en el lenguaje.
Entonces en esos casos se hace alusión, inducir para explicar lo que se quiere decir con esa palabra.
El concepto es predicativo, es la referencia de un predicado gramatical.
Cópula es la palabra que une dos términos de la oración o dos oraciones.
Una ecuación es reversible, el caer un objeto bajo un concepto no es una relación reversible.
Distinguir entre la relación: caer un objeto bajo un concepto.
Y la relación: estar un concepto subordinado a otro concepto.
Ejemplo:
En el enunciado “el lucero matutino es Venus”, tenemos dos nombres propios para el mismo objeto.
En el enunciado “el lucero matutino es un planeta”, tenemos un nombre propio: “el lucero matutino” y un término conceptual: “un planeta”.
El “es” en: “el lucero matutino es Venus”, no es sólo una mera cópula, también es una parte esencial del predicado, de modo que en la palabra “Venus” no está contenido el predicado entero.
Pues se podría decir: “el lucero matutino no es sino Venus”, y aquí hemos descompuesto en tres palabras lo que antes radicaba en el simple “es”, y en “no es sino” el “es” es ya sólo cópula. Lo que aquí se ha expresado no es pues Venus, sino no es sino Venus.
Estas palabras se refieren a un concepto, bajo el cual claro está sólo cae un único objeto.
Este concepto debe distinguirse del objeto. La palabra “Venus” nunca podrá ser un predicado pero puede formar parte de un predicado.
La referencia de esta palabra no puede aparecer nunca como concepto, sino sólo como objeto.
Un concepto puede caer bajo uno superior, lo cual, no tiene que ser confundido con la subordinación de un concepto bajo otro. (relaciones entre conceptos)
El artículo determinado siempre indica un objeto, mientras que el indeterminado acompaña a un término conceptual.
No pocas veces hay algo de común en diferentes expresiones, esto es lo que llamo el sentido y, para los enunciados en particular, el pensamiento.
Se puede expresar diferentemente el mismo sentido, el mismo pensamiento, pues, la diferencia es sólo de la concepción, la ilustración, la matización del sentido, y ésta no entra en consideración para la lógica.
Entendiendo “predicado” y “sujeto” en el sentido lingüístico: concepto es la referencia de un predicado, mientras que objeto es lo que nunca puede ser toda la referencia de un predicado, aunque puede ser la referencia de un sujeto.
Las palabras “todos”, “cada”, “ningún” aparecen delante de términos conceptuales.
Las relaciones entre conceptos y su naturaleza particular
Ejemplo:
En el enunciado: “todos los mamíferos son terrestres”
Formas de negación:
Todos los mamíferos no son terrestres.
No todos los mamíferos son terrestres. (aquí todos pertenece al predicado)
Ahora bien, por el contrario, negamos el enunciado:
“el concepto de mamífero está subordinado al concepto terrestre”, negando el predicado: “no está subordinado al concepto terrestre”.
El señor Frege usa expresiones como “el concepto F” no designan conceptos, sino objetos. Podemos sustituir “extensión del concepto” por “concepto”.
(Concepto y objeto). He llamado a la existencia propiedad de un concepto.
Ejemplo: En el enunciado, “hay por lo menos una raíz cuadrada de 4”.
No se afirma nada del número determinado 2, ni del -2, sino de un concepto, a saber, raíz cuadrada de 4.
Pero si expreso el mismo pensamiento así: “el concepto raíz cuadrada de 4 es satisfecho”, las primeras seis palabras constituyen el nombre propio del objeto.
Un pensamiento puede ser descompuesto de múltiples maneras y que, por eso, unas veces aparece una cosa, otras, otra como sujeto o como predicado.
Se designa algo determinado únicamente cuando al mismo tiempo, se señala un determinado modo de descomposición.
Diferentes enunciados pueden expresar el mismo pensamiento. Para nuestro anterior pensamiento también encontrarse una aseveración sobre el número 4 del tipo:
“el número 4 tiene la propiedad de que hay algo de lo cual es su cuadrado”.
La distinción de formas de la activa y la pasiva.
Un mismo pensamiento puede aparecer en una descomposición como singular, en otra como particular, y en una tercera como universal.
Un nombre propio no puede ser nunca una expresión predicativa.
La lengua utiliza a veces la misma palabra en parte como nombre propio y en parte como término conceptual.
En general: el concepto se comporta de modo esencialmente predicativo.
La aserción que se hace sobre un concepto, no es en absoluto adecuada para un objeto.
Los conceptos de segundo orden, bajo los cuales caen conceptos, son esencialmente distintos de los conceptos de primer orden, bajo los cuales caen objetos.
La relación de un objeto con un concepto de primer orden bajo el cual cae es distinta, aunque parecida, a la relación de un concepto de primer orden con un concepto de segundo orden.
Quizá se podría decir, que un objeto cae bajo un concepto de primer orden, y que un concepto cae en un concepto de segundo orden.
La diferencia entre concepto y objeto es completamente tajante.
Las palabras “propiedad” y “característica”
Ejemplo:
“2 es un número positivo” y
“2 es un número entero” y
“2 es menor que 10”,
también podemos decir
“2 es un número entero positivo menor que 10”
Aquí aparecen: ser un número positivo, ser un número entero, ser menor que 10, como propiedades del objeto 2, pero al mismo tiempo como características del concepto, número positivo menor que 10. Este concepto no es ni positivo, ni un número entero, ni menor que 10. Ciertamente está subordinado al concepto número entero, pero no cae bajo éste.
Un medio de conexión
Ejemplo:
“el número 2” no se engancha al de la expresión “el concepto número primo” sin un medio de conexión.
Tal medio lo empleamos en el enunciado “el número 2 cae bajo el concepto de número primo”. Se halla contenido en las palabras “cae bajo”, las cuales necesitan de complementación en un doble sentido: por un sujeto y por un acusativo; y, únicamente porque su sentido es no-saturado, son aptas para servir de medio de conexión.
Tan sólo cuando han sido completadas en ese doble aspecto, tenemos un sentido cerrado, tenemos un pensamiento.
“Cerrado” y “no-saturado” son expresiones intuitivas.
Prólogo a “las leyes fundamentales de la aritmética”.
Al conjunto de los signos especiales que uso para demostrar teoremas de la aritmética los llamo ideografía.
(Pensamiento de Frege) El ideal de un método estrictamente científico de la matemática
Exijo que se mencionen previamente todos los modos de deducción y de inferencia que se empleen.
El señor Frege expresa la fórmula “A” implica la fórmula “B” (en nuestra notación actual A → B) de la siguiente manera:
![]()
Por esto llama a “A” el “miembro inferior” (en una inferencia) y a “B” el “superior”
Tabla con las distintas notaciones:
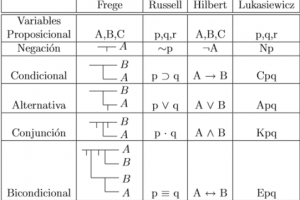
La elección de una demostración para llevar a cabo una prueba. El conjunto de los modos de deducción e inferencia admitidos.
Con que no haya lagunas en las cadenas deductivas se consigue poner de manifiesto cada axioma, presupuesto, hipótesis sobre los que se base una demostración, y así obtenemos un fundamento para el enjuiciamiento de la naturaleza epistemológica de la ley demostrada.
La aritmética es en gran parte lógica desarrollada. Por ejemplo, en el momento en que ciertos pasos se descompongan en pasos lógicos simples.
Otros aspectos como comprobar si una cadena deductiva es concluyente o de si unas premisas son sólidas.
Poder indicar exactamente dónde se halla el error según:
- En las leyes fundamentales
- En las definiciones
- En las reglas o en su aplicación en un determinado lugar
Los fundamentos sobre los que se basa cada teorema en particular.
La ley fundamental de los recorridos (V) de Frege habla por ejemplo de extensiones de concepto, de forma puramente lógica.
Las exigencias de rigor en las demostraciones tienen como consecuencia ineludible una mayor longitud de las pruebas.
No caer en el error común aceptado de comprender la prueba inmediatamente en un único acto cognoscitivo.
Ver Dedekind (“Qué son y qué deben ser los números”), sobre la fundamentación de la aritmética.
El señor Dedekind también es de la opinión de que la teoría de los números es una parte de la lógica.
Los matemáticos acostumbran a estar interesados solamente en el contenido del teorema y en que sea probado.
A diferencia el señor Frege lo nuevo no es el contenido del teorema, sino el modo como se lleva a cabo la prueba, los fundamentos sobre los que se apoya.
Ver los Fundamentos de la aritmética del año 1884, Breslau, edición de Wihelm Koebner, del señor Frege.
En su concepción sobre el número, lo fundamental de sus resultados lo expresó diciendo que la asignación de número es una aserción sobre un concepto.
¿Qué es asignar un número y cómo se debe asignar un número?
La concepción, la fundamentación mediante signos un sistema.
En el lenguaje natural también aquí, al asignar un número se nombra siempre un concepto.
Recorrido de una función. Definiciones de la univocidad de una relación.
Frege define el número mismo como una extensión de concepto y las extensiones de concepto son recorridos.
Enunciado afirmativo:
- El reconocimiento de su verdad
- El contenido que se reconoce como verdadero.
Al contenido lo llamo pensamiento y valor veritativo.
Esto es consecuencia de la distinción entre sentido y referencia de un signo.
El pensamiento, que en los demás casos es el sentido del enunciado, pasa a ser, en el estilo indirecto, su referencia.
“Los conceptos y las relaciones son funciones en el sentido ampliado”, conferencia de Frege sobre “Función y concepto”.
El rigor de las cadenas deductivas.
Los modos de inferencia y de deducción.
En el contexto de la ideografía los signos formados regularmente deben referirse a algo, principio que es esencial para conseguir un rigor absoluto.
Los objetos de la aritmética, los números, son de naturaleza no-sensible.
Se toman los signos numéricos por los números.
Los signos tienen propiedades totalmente distintas de las de los números.
Es un enigma cómo puede tener lugar una definición cuando se prescinde de cualquier conexión entre signo y designado.
Se afirma la existencia señalando la tangibilidad de los signos.
¿Qué es definir? ¿Qué se puede conseguir mediante definiciones?
La falta de distinción entre concepto y objeto.
Ejemplo: “un cuadrado es un rectángulo en el que los lados que se tocan son iguales”, se define el concepto (cuadrado), al indicar las propiedades que algo debe tener para caer bajo este concepto. A estas propiedades las llamo características del concepto. (Estas características del concepto no son sus propiedades)
Crear el cero es, pues, imposible, ni el concepto, definido tiene esta propiedad, ni la definición garantiza que el concepto no sea vacío.
Diferencia entre la característica de un concepto y la propiedad de un objeto.
Las leyes lógicas deben ser pautas del pensamiento para alcanzar la verdad.
“Leyes del pensamiento” vistas como las más generales, que siempre que se piensa prescriben cómo hay que pensar.
¿Prescriben cómo hay qué pensar?
¿De qué lógica o de qué tipo de lógica de naturaleza de lógica hablamos? ¿Lógica psicológica?
La verdad y la validez general. El acuerdo general
Los individuos reducen y muchas veces confunden la verdad con la aquiescencia o consentimiento.
Los lógicos psicologistas (falta de claridad) tienden a confundir la verdad en sí misma, es decir, el ser verdad en sí mismo es no-espacial y atemporal, la confunden con su lógica psicológica con leyes que tratan de hombres y contiene una determinación temporal.
Observamos que si una verdad se refiere a algún tipo de circunstancia como lugar y tiempo determinados en alguna medida esta pertenece al ámbito o naturaleza del hombre y no del universo.
Otro aspecto es el individuo que duda de una ley, por ejemplo, la que obedece la ecuación de Pitágoras que este retomó de los egipcios y estamos hablando de hace cuatro mil años como mínimo.
Lo que no es prudente es tener por verdad algo que nace en nuestras creencias, pasiones sin someterlas a juicio racional dentro de la lógica pura.
El origen de la polémica es la distinta concepción de lo verdadero.
Lo objetivo.
Yo admito un dominio de lo objetivo no-real, mientras que los lógicos psicologistas consideran lo no-real como subjetivo sin más.
Se debe comenzar el análisis explicando definiendo objeto y representación-representado.
Así separamos lógica pura, de la psicológica.
¿Hay una auténtica objetividad?
Se habla de un objeto de representación, si bien el objeto mismo ha de ser una representación.
Este sería, pues, una representación de representación.
Hemos usado las palabras “objeto”, “realidad”, “sujeto”, “sujeto material”, “juicio”, “representación”, “trascendente”, “fundamento óntico”, “representado”, “subjetivo”, “objetivo”.
¿Qué se saca en claro de todo esto? Que la lógica psicologista va a la deriva al concebir sujeto y predicado de los juicios como representaciones en el sentido de la psicología, que las consideraciones psicológicas son tan inadecuadas en lógica, como lo son en astrofísica o geología.
Si queremos salirnos de lo subjetivo, debemos concebir el conocimiento como una actividad que no produce lo conocido, sino que agarra algo que ya existe.
Lo que aprehendemos mentalmente existe independientemente de esta actividad, por tanto, un concepto es independiente del ser humano, existe independientemente también de las representaciones y de sus cambios, que pertenecen o acompañan a esta aprehensión; no es ni el conjunto de estos procesos internos del individuo, ni es producido por ellos como parte nuestra vida mental.
Para los lógicos psicologistas todo es representación. Para ellos un tipo al menos de existencia es confundida con la realidad, que, no es distinguida claramente de la objetividad.
¿De qué cosa afirmamos propiamente que es real cuando decimos que hay raíces cuadradas de cuatro?
Primero hay que haber comprendido la diferencia entre conceptos de primero y segundo orden, cosa que la lógica psicologista es sin duda incapaz.
Mientras el matemático define objetos, conceptos y relaciones, el lógico psicologista espía el devenir y la transformación de las representaciones, y en el fondo, las definiciones del matemático no pueden parecerle sino insensatas, porque no reflejan la esencia de la representación.
[Después de ver que la psicología actualmente está tan sólo preocupada por la humanidad de forma subjetiva, pues, lo vemos en los libros, prensa, noticias, donde prima el carácter sensacionalista. Observo que la psicología tiene gran responsabilidad en la parte del proceso de transmitir la información al ciudadano, utilizando el escudo del nombre de la ciencia. Jesús Díaz]
Introducción a las Leyes Fundamentales de la Aritmética
Hay que determinar previamente un conjunto de modos de deducción y de inferencia, y no hay que dar ni un paso que no siga esos modos.
En esta forma de demostración, no es suficiente con que el paso aparezca como correcto, sino que hay que descomponerlo en los pasos lógicos simples de que está compuesto, y a menudo éstos son no pocos.
Hay que descubrir cada axioma que nos sea preciso. Necesitamos una clara comprensión de la naturaleza epistemológica de una ley. Dos conceptos deben ser concebidos con rigor.
- Schröder, en sus Conferencias sobre el Álgebra de la lógica (Leipzig, 1890,p.253), da un paso más allá que Dedekind, al hacer notar la conexión de los sistemas de éste con los conceptos, conexión que Dedekind parece haber pasado por alto.
Ver demostración dentro de las álgebras de Lie.
Lo que Dedekind realmente quiere decir, cuando dice que un sistema es parte de otro sistema, es la subordinación de un concepto bajo otro concepto o al caer un objeto bajo un concepto, dos casos diferentes, que ni él ni Schröder distinguen en absoluto, a consecuencia de un error de concepción común a ambos; pues también Schröder considera sus elementos, en el fondo, como lo que constituye su clase.
En rigor, tan ilícitas son en la teoría de Schröder las clases vacías, como en la de Dedekind los sistemas vacíos; pero la necesidad de ello, que surge de la naturaleza misma de la cuestión, se impone en ambos autores de manera diversa.
Recordemos: lo que constituye un concepto son los objetos que caen bajo el concepto y no las características que caen bajo un concepto.
Si es correcta mi idea de que la aritmética es una rama de la lógica, entonces habrá que elegir en vez de “aplicación” una expresión puramente lógica. Y escojo la de “relación”.
Concepto y relación son las piedras fundamentales sobre las que constituyo mi edificio.
Para explicar y desarrollar la cuestión paulatinamente, no debo y no trataré de alcanzar desde el principio la plena generalidad ni la expresión definitiva.
El uso de las comillas,
Con ellas distingo los casos en que hablo de los signos mismos de aquellos en que hablo de su referencia.
Hablar o escribir inexacto,
Puede llegar a confundir el pensamiento. Por ejemplo, se han tomado los signos numéricos por los números, el nombre por lo denominado, el mero instrumento por el verdadero objeto de la aritmética.
¿Qué es una función?
La expresión de cálculo y la expresión de variable.
El concepto de constante, invariable o fijo y el concepto de variación o variable.
Diversas propiedades o estados del mismo objeto. El sujeto y su variación. Un objeto toma una propiedad.
El número en cuanto objeto se le llama variable o magnitud variable; como propiedad, se le llama valor.
Se prefiere la palabra “magnitud” a la palabra “número”.
Las variables o magnitudes variables no pertenecen al análisis puro. Números variables no existen.
¿Cómo pasamos de las variables a la función?
La expresión de cálculo, como grupo de signos, no pertenece en realidad, a la aritmética.
Analicemos los componentes o partes de la expresión:
“y = x² + 3x”, se compone de signos numéricos, signos de cálculo y la letra “x”.
No siempre se ha distinguido claramente entre signos y designado.
En “x² + 3x”, la letra “x” sólo alude, no se refiere a nada.
¿Pero dónde queda la función?
El paso de un signo que alude a un signo que designa.
Observación: considerar la introducción de nuevos símbolos en el lenguaje simbólico de la aritmética.
El signo de una función
El signo de una función nunca está saturado, necesita ser completado por medio de un signo numérico, que entonces llamamos signo del argumento.
Las expresiones inexactas producen definiciones defectuosas.
Crear un lenguaje matemático que conjugue la exactitud más rigurosa con la mayor brevedad posible. Tal vez una ideografía, un conjunto de reglas, según las cuales, por medio de signos escritos o impresos, puedan expresarse directamente los pensamientos, sin mediación de la voz.
Términos
Aquiescencia: Asenso, consentimiento.
Prescribe: Ordenar, determinar algo. Dicho de un derecho, de una responsabilidad o de una obligación. Extinguirse por haber transcurrido cierto período de tiempo, especialmente un plazo legal.
Óntico: Del ser(ente) o relacionado con él.
Bibliografía
Conferencias sobre el álgebra de la lógica (lógica exacta), Schröder 1891.
Frege, Ideografía
V. E. Heine: “Los elementos de la teoría de funciones”
B. Erdmann Lógica, Halle a.S., Max Niemeyer 1892
