Álgebras | UnIG

Álgebra geométrica

ÁLGEBRAS DE KOSZUL

Álgebra de Clifford

Es un álgebra basada en el producto geométrico, una generalización del producto escalar y del producto vectorial operando sobre multivectores. Un multivector es la generalización n-dimensional del concepto de vector. Ver álgebra geométrica.

Sea V un espacio vectorial sobre un cuerpo k y q : V → k una forma cuadrática en V. El álgebra de Clifford C(q) es un álgebra asociativa unital sobre k junto con la función lineal i: V → C(q) definido por la propiedad universal siguiente: para cada álgebra asociativa A sobre k con una función lineal j: V → A tal que para cada v en V se tiene j(v)² = q(v)1 (donde 1 denota la identidad multiplicativa de A), hay un homomorfismo único del álgebra f: C(q) → A tal que el diagrama siguiente conmuta

${\begin{matrix}V&\to &C(q)\\\downarrow &\swarrow &\\A&&\end{matrix}}$ ${\begin{matrix}V&\to &C(q)\\\downarrow &\swarrow &\\A&&\end{matrix}}$

es decir tal que fi = j.

El álgebra de Clifford existe y puede ser construida como sigue: tome el álgebra tensorial T(V) construida por el ideal generado por

$v\otimes v-q(v)1$ $v\otimes v-q(v)1$ .

Se sigue de esta construcción que i es inyectivo, y V se puede considerar como subespacio lineal de C(q).

Sea

B(u, v) = q(u + v) – q(u) – q(v)

la forma bilineal asociada a q. Que es una consecuencia de la definición que la identidad

uv + vu = B (u, v)

vale en C(q) para cada par (u, v) de vectores en V. Si el cuerpo es de característica distinta de 2 esta expresión se puede utilizar como definición alternativa.

El álgebra de Clifford C(q) es filtrada por subespacios

k ⊂ k + V ⊂ k + V + V² ⊂ …

de los elementos que se pueden escribir como monomios de 0, 1, 2,.. vectores en V. El álgebra graduada asociada es canónicamente isomorfa al álgebra exterior Λ V del espacio vectorial. Esto muestra en particular que

dim C(q) = 2^{dim V}.

Una manera más simple de considerar esto es eligiendo una base arbitraria e₁, e₂….. para V. Usando la relación de anticonmutación podemos expresar siempre un elemento del álgebra de Clifford como combinación lineal de monomios del tipo

$e_{i_{1}}e_{i_{2}}e_{i_{3}}\cdots e_{i_{n}},i_{1}<i_{2}<\cdots <i_{n}$ $e_{i_{1}}e_{i_{2}}e_{i_{3}}\cdots e_{i_{n}},i_{1}<i_{2}<\cdots <i_{n}$

que da un isomorfismo explícito con el álgebra exterior. Obsérvese que éste es un isomorfismo de espacios vectoriales, no de álgebras.

Si V tiene dimensión finita par, el cuerpo es algebraicamente cerrado y la forma cuadrática es no degenerada, el álgebra de Clifford es simple central. Así por el teorema de Artin-Wedderburn es (no canónicamente) isomorfa a un álgebra de matrices. Se sigue que en este caso C(q) tiene una representación irreducible de dimensión 2^dim(V)/2 que es única salvo un isomorfismo (no único). Éste es la famosa representación por espinor), y sus vectores se llaman espinores.

En caso de que el cuerpo k sea el cuerpo de números reales el álgebra de Clifford de una forma cuadrática de signatura p, q es generalmente denotada C(p, q). Se han clasificado estas álgebras reales de Clifford como sigue…

Las álgebras de Clifford son importantes en la física. Los físicos consideran generalmente las álgebras de Clifford expresadas por las matrices γ₁…,γ_n que tienen la propiedad que

γ_i γ_j + γ_j γ_i = 2δ_i,j

donde δ es la matriz de una forma cuadrática del tipo p,q con respecto a una base ortonormal de e₁,…, e_n.

Álgebra Graduada

Las álgebras por sí mismas se han estudiado a fondo durante mucho tiempo. El propósito de las graduaciones es ir un paso más allá e investigar de qué manera se pueden descomponer las álgebras. Para que una descomposición sea válida, vamos a requerir que sea compatible con las operaciones del álgebra. La definición precisa de calificación en un álgebra D por un grupo G consta de dos partes. Primero, la calificación como tal es simplemente una descomposición del espacio vectorial subyacente de D en una suma directa de subespacios vectoriales, de modo que cada subespacio vectorial está indexado por un elemento del grupo G.

ÁLGEBRA DE HEYTING

Las álgebras de Heyting son una generalización del álgebra de Boole que modela lógica proposicional intuicionista.

ÁLGEBRA DE HOPF

Álgebra de Steenrod

Definición. El álgebra de Steenrod se presenta como un subálgebra del álgebra de endomorfismos de un functor. El functor en cuestión asigna a un espacio vectorial sobre un cuerpo de Galois el álgebra de funciones polinomiales en ese espacio vectorial: el subálgebra de los endomorfismos de este functor que resulta en es un álgebra de Steenrod si el cuerpo base es el primer cuerpo, generado por los componentes homogéneos de una variante del mapa de Frobenius.

ÁLGEBRAS DE WEYL

Nota: Las álgebras de Weyl generalizadas desde un punto de vista homológico.

Estas álgebras se construyen a partir de una k-álgebra D, un automorfismo σ:D→D y un elemento central a∈Z(D). Están generadas por D y dos variables x e y sujetas a las relaciones:
dy=yσ(d), xd=σ(d)x, yx=a, xy=σ(a), para d∈D.
Las álgebras de Weyl generalizadas fueron introducidas por Bavula en el contexto de álgebras de operadores diferenciales.

Álgebras de Yang-Mills

Las álgebras de Yang-Mills son álgebras de Koszul cúbicas, de dimensión global 3 y son álgebras envolventes de álgebras de Lie.

Definición

Sea n ∈ N y sea f(n) el álgebra de Lie libre con n generadores {x1, . . . , xn}. Se trata de una k-álgebra de Lie de dimensión infinita provista de una graduación sobre N localmente de dimensión finita. El álgebra de Yang-Mills con n generadores se define como el álgebra de Lie sobre k

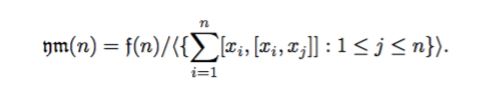
Notemos que Nm(n) es un álgebra de Lie con una N-graduación localmente de dimensión finita, por ser cociente de un álgebra de Lie con una N-graduación localmente de dimensión finita por un ideal homogéneo.