Álgebras de Lie

Introducción

 

La clasificación de grupos de Lie proporciona la lista de los posibles grupos existentes de simetrías infinitesimales, válidos para eventuales y futuros modelos científicos.

 

El origen de  las    álgebras  de  Lie  está  en la   Geometría   y   las  Ecuaciones   Diferenciales.    Sophus Lie   estudió   los trabajos   de   Evariste Galois   y    encontró   semejanzas   entre la  teoría   de   Galois  sobre resolubilidad  de  ecuaciones y  la resolución  de  ciertas  ecuaciones  diferenciales.  La estructura de grupo será entonces muy importante.

 

Esto le llevo al concepto de “transformaciones infinitesimales” (o campos vectoriales), que formaban    un sistema cerrado para el corchete: [x, y]=xy−yx. Tras los trabajos de Weyl, hacia 1930, los grupos continuos de transformaciones pasaron a ser llamados grupos de Lie, y sus “grupos infinitesimales” álgebras de Lie.

En la  notación  actual ,  lo que  Lie  consideró son  los  actuales    “grupos de Lie locales”   y  sus álgebras de Lie, que los determinan. define el concepto de álgebra de Lie y clasifica las álgebras de Lie simples de dimensión finita.

 

Elie Cartan obtiene la completa clasificación de las álgebras de Lie simples complejas en  su  tesis.   (Uno de los grandes descubrimientos en matemáticas de todos los tiempos.)

 

La clasificación de Killing-Cartan de álgebras de Lie simples basada en espacios raíces.

 

Otra versión:

Álgebras Asociativas y Álgebras de Lie

 

Definición 1.1.1

Un  álgebra  es un  espacio vectorial  A  sobre  un cuerpo  F  junto con una aplicación  bilineal  m: \(A \times A \rightarrow A\)

A la aplicación bilineal m de la definición anterior se le llama multiplicación. Si A es un álgebra y \(x, y \in A\) normalmente escribimos xy en lugar de m(x,y).

Como un álgebra A es un espacio vectorial, podemos considerar los subespacios de A.

A un subespacio \(B \subset A\)  se  le  llama   subálgebra                                     si  \(x y \in B \quad \forall x, y \in B.\)

 

 

Se dice que es un ideal si   xy  e  yx  están en B  \(\forall x \in A\quad y\quad \forall y \in B\).  Claramente un ideal es por tanto un subálgebra.

Sean A y B dos álgebras sobre el cuerpo F. Una aplicación lineal   \(\theta : A \rightarrow B\)   se dice que es un morfismo de álgebras  si   \(\theta(x y)=\theta(x) \theta(y) \quad\)  \(\forall x, y \in A \quad (x y \in A, \theta(x) \theta(y) \in B)\).

La aplicación \(\theta\) es un isomorfismo de álgebras si \(\theta\) es biyectiva.

Definición 1.1.2  Un álgebra A se dice que es asociativa si para \(\forall x, y, z \in A\) tenemos

\((x y) z=x(y z) \quad\) (ley asociativa)

 

Definición 1.1.3   Un álgebra L se dice que es un álgebra de Lie si la multiplicación cumple las siguientes propiedades:

L1)   xx = 0  \(\forall x\in L\),

L2)   x(yz) + y(zx) + z(xy) = 0    \(\forall x,y,z \in L\)      (Identidad de Jacobi)

 

Sea L un álgebra de Lie y sea (x,y\in L). Entonces 0 = (x +y )(x + y) = xx + xy + yx + yy = xy + yx. Por tanto la condición (L1) implica     xy = -yx  \(\forall x,y\in L\)    (1.1)

Por otro lado (1.1) implica  xx = -xx, o 2xx = 0 \(\forall x\in L\).  La conclusión es que si la característica del cuerpo no es 2, entonces (L1) es equivalente a (1.1). Usando (1.1) vemos que la identidad de Jacobi es equivalente a:

(xy)z + (yz)x + (zx)y = 0  \(\forall x,y,z\in L\).

Ejemplo 1.1.4   Sea V un espacio vectorial de dimensión n sobre el cuerpo F. Consideremos el espacio vectorial End(V) de todas las aplicaciones lineales de V en V.  Si \(a, b \in End(V)\) entonces su producto está definido por

ab(v)  =  a(b(v))  \(\forall v\in V\).

Esta multiplicación convierte End(V) en un álgebra asociativa.

Sean \(a, b \in End(V)\)  definimos [a,b] = ab – ba   la aplicación bilineal \((a, b) \rightarrow[a, b]\)  se llama el conmutador, o el corchete de Lie.  El espacio de aplicaciones lineales de V en V junto con el corchete es un álgebra de Lie y se denota por \(g l(\boldsymbol{V})\).

Proposición 1.1.5   Sea A un álgebra y  \(B \subset A\)  un ideal.  Sea A/B el espacio cociente. Entonces la multiplicación sobre A induce a la multiplicación sobre A/B  por  \(\overline{x} \overline{y}=\overline{x y}\)  (donde \(\overline{x}\) el representante de \(x\in A\) en A/B).  Por lo tanto, si A es un álgebra de Lie, entonces también lo es A/B (igualmente si A es un álgebra asociativa).

De un álgebra de Lie podemos construir un álgebra asociativa.   Sea L un álgebra de Lie sobre el cuerpo F.  Para \(x \in L\)  definimos una aplicación lineal

\(a d_{L} x : L \rightarrow L\)

para    \(a d_{L} x(y)=[x, y]\)   para  \(y \in L\).  Esta aplicación se llama la aplicación adjunta determinada por x.

Consideremos el subálgebra de  End(L)  generado por la aplicación identidad junto con  \(\{a d x | x \in L\}\)  (por ejemplo el subálgebra más pequeño de End(L) conteniendo a 1 y su conjunto).

Este álgebra asociativo se denota por   \((a d L)^{*}\).

A menudo estudiaremos la estructura del álgebra de Lie L investigando su aplicación adjunta. Esto nos permitirá usar herramientas del álgebra lineal. (ver nilradical sección 2.2).

 

1.2 Álgebras de Lie lineales.

Por \(E_{i j}^{n}\) denotaremos la matriz nxn con 1 en la posición (i,j) y 0 en otras posiciones.

Una base de \(gl_{n}(F)\) está formada por todos  \(E_{i j}\)    para  \(1 \leq i \leq n\)    y   \(1 \leq j \leq n\)

Recordar que \(gl_{n}(F)\) es el álgebra de Lie de todas las matrices nxn con coeficientes en el cuerpo F.

Por lo tanto, las subálgebras de \(gl_{n}(F)\) se llaman las álgebras de Lie lineales.

Sea V un espacio vectorial de dimensión n sobre el cuerpo F.  Recordamos que una forma bilineal f sobre V es una función bilineal  \( f : V \times V \rightarrow F \).

Es simétrica si  f(v,w) = f(w,v)  y  antisimétrica si  f(v,w) = -f(w,v)    \(\forall v,w\in V\).   Además, f se dice que es no degenerada si  f(v,w) = 0   \(\forall w\in V\) implica que v = 0.   Definimos el conjunto de las formas bilineales f  en  V

\( L _ { f } = \{ a \in g l ( V ) \ | \ f ( a v , w ) \ = \ – f ( v , a w ) \ \ \ \forall v , w \in V \} \ \ \ \ (1.3) \)

que es el subespacio lineal de \(gl(V)\).

Lema 1.2.2  Sea f una forma bilineal sobre el espacio vectorial V de dimensión n.  Entonces \( L _ { f }\)  es un subálgebra de \(gl(V)\).

\( Tomando \  L _ { f } , \  M _ { f } = \left( \begin{array} { c c } { 0 } & { I _ { l } } \\ { – I _ { l } } & { 0 } \end{array} \right) , \  I _ { l } \)    denota la matriz identidad   \( l \times l \)

\( a \in g l _ { 2 l } ( F ) , \ \ \ a = \left( \begin{array} { c c } { A } & { B } \\ { C } & { D } \end{array} \right) , \  A , B , C , D \)    son matrices   \( l \times l \)

Expandiendo la condición    \( a ^ { t } M _ { f } = – M _ { f } a \)   obtenemos  \(B\) = \(B ^ { t }\),  \(C\) = \(C ^ { t }\)  y  \(D\) = \(-A ^ { t }\).

Con las matrices \(A_{ ij }\), \(B_{ ij }\) y \(C_{ ij }\)  obtenemos las bases de \(L_{f }\),

y finalmente encontramos la dimensión de \(L_{f}\) que es  \(2l^ {2} + l\).

Este álgebra de Lie se llama el álgebra de Lie simpléctico y se denota  \( s p _ { 2 l } ( F ) \).

 

A partir de un álgebra asociativa siempre podemos definir un álgebra de Lie.

Un álgebra de Lie no puede ser asociativa en general.

Todo ideal es una subálgebra pero el inverso no es cierto.
En un álgebra de Lie solo hay una clase de ideales (biláteros,por la
antisimetría del producto). Ideal bilátero (simultáneamente por la derecha e izquierda).

La relación entre homomorfismos e ideales biláteros es muy importante en la teoría
de representaciones. Nótese que en general no es posible construir un álgebra cociente
utilizando una subálgebra.

Subálgebras de álgebras de Lie simples
La caracterización de las subálgebras maximales de un álgebra de Lie simple tiene muchas
aplicaciones en física. Como ejemplo, considérese el modelo standard de la teoría de unificación
en partículas elementales y la inclusión:
SU(5) ⊃ SU(3)×SU(2)×U(1)

 

The space G/B and its fibrations
Let G be the group SL(3,C), and B the subgroup of lower triangular matrices.

Dolbeault complex for X
holomorphic differentials

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

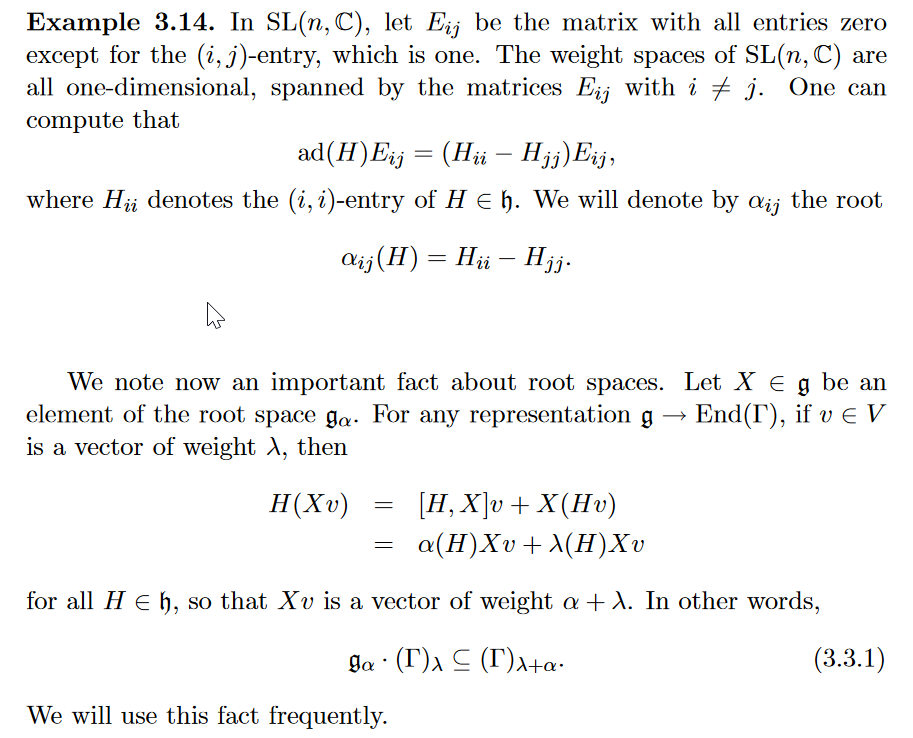
CASO A

Mostrar que el álgebra de Lie de Yang-Mills tiene como sumando directo a un ideal que en sí mismo es un álgebra de Lie libre.
Nociones de graduación y filtración.
Representaciones de álgebras de Lie, y los resul- tados sobre su homología y cohomología
La noción de polarización de funcionales lineales.
Ideales maximales del álgebra envolvente de un álgebra de Lie nilpotente.

Álgebra de Hopf
Definiciones de álgebras y coálgebras en categorías monoidales
Sea C una categoría k-lineal de Grothendieck: objeto graduado, componente (homogénea), objeto producto tensorial, funtor de suspensión, funtor de homología, álgebra aumentada,
coálgebra coasociativa

Álgebras diferenciales graduadas situándolas en el contexto de las A∞-álgebras y A∞-coálgebras, debidas a ( Stasheff )
La familia de morfismos {mi}i∈N, define en A una estructutra de A∞-álgebra.
Construcción bar de A
Funtor plenamente fiel B : Alg∞ → Cogc, que preserva homotopías

Filtraciones
Sea ahora A la categoría Gr(C) o C(C). Una filtración de un objeto M de A es una sucesión creciente de subobjetos de M
indexada por N0. Diremos que la filtración es exhaustiva si
F0M ⊆F1M ⊆···⊆FiM ⊆···⊆M colim FiM = M, →N0 y admisible si es exhaustiva y F0M = 0.

 

CASO B

Mostrar que el álgebra de Lie de Yang-Mills tiene como sumando directo a un ideal que en sí mismo es un álgebra de Lie libre.
Nociones de graduación y filtración.
Representaciones de álgebras de Lie, y los resul- tados sobre su homología y cohomología
La noción de polarización de funcionales lineales.
Ideales maximales del álgebra envolvente de un álgebra de Lie nilpotente.

 

CASO C

Una subálgebra de Cartan t de sp(V) son los operadores en sp(V) cuya matriz en la base B es diagonal.
Las raíces de un álgebra de Lie simple g es un conjunto finito Φ(g,t) de funcionales lineales en una subálgebra de Cartan t.